Etude du tube témoin.
a) Étude mathématique.
Pour notre expérience à 25 degrés, nous avons vu que la croissance suivait une droite. Cependant, nous possédons un nuage de point, et, afin de pouvoir réaliser un ajustement affine pour obtenir le meilleur ajustement possible, qui consiste à calculer les résidus, c'est-à-dire l’écart qu’il y a entre les points et la droite tracée. Pour cela nous avons choisi de tracer une droite passant par deux point nommés A et B. Nous calculerons ensuite l’équation de cette droite telle que y= ax+b
Avec :
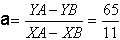
Et b étant l’ordonnée à l’origine de la courbe : b=160.
Nous pouvons donc donner y=65/11 x + 160
La deuxième colonne du tableau représente les abscisses des points placés. La troisième colonne l’ordonnée de ces mêmes point. La quatrième est le calcul de y en remplaçant x par les valeurs Xi. La cinquième colonne est le carré (pour ne pas avoir de valeurs négatives) de la différence des écarts entre Yi et y. La sixième colonne correspond a la somme des résultats en cinquième colonne pour connaître la somme des résidus. Plus cette valeur est basse plus la droite est meilleure.
| Xi | Yi | y=65/11 Xi+160 | (Yi-y)2 | Résidus | |
| A | 18 | 250 | 266.364 | 267.769 | 817.339 |
| B | 90 | 695 | 691.818 | 10.124 | |
| C | 0 | 160 | 160.000 | 0.000 | |
| D | 24 | 290 | 301.818 | 139.669 | |
| E | 42 | 420 | 408.182 | 139.669 | |
| F | 66 | 550 | 550.000 | 0.000 | |
| G | 74 | 582 | 597.273 | 233.256 | |
| H | 97 | 728 | 733.182 | 26.851 |
Cependant, pour voir s’il est possible d’avoir de meilleurs résultats, nous allons donc utiliser une autre méthode nommée la méthode de Meyer étant également un ajustement affine mais consistant à séparer le nuage de point du départ en deux sous nuage. Nous calculerons ensuite la moyenne des abscisses, puis des ordonnées de ces points pour n’avoir au final que deux points moyens de deux sous nuages que l’on nommera G1 et G2.
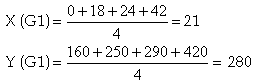
G1 a pour coordonnées G1 (21 ; 280). Nous effectuerons de même pour G2 :
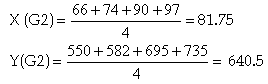
G2 a donc pour coordonnées G2 (81.75 ; 640.5) Ayant désormais les coordonnées de ces deux points nous pouvons calculer l’équation de la droite passant par ces deux points : y G = ax+b
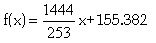
Nous pouvons maintenant dresser le tableau permettant de calculer les résidus.
| Xi | Yi | f(x)=1444/253*Xi+155.382 | (Yi-f(x))*(Yi-f(x)) | Résidus. | |
| A | 18 | 250 | 262.345 | 152.398 | 679.266 |
| B | 90 | 695 | 690.197 | 23.071 | |
| C | 0 | 160 | 155.382 | 21.326 | |
| D | 24 | 290 | 297.999 | 63.989 | |
| E | 42 | 420 | 404.962 | 226.134 | |
| F | 66 | 550 | 547.580 | 5.859 | |
| G | 74 | 582 | 595.119 | 172.098 | |
| H | 97 | 728 | 731.794 | 14.391 | |
| G1 | 21 | 280 | 280.000 | 0 | |
| G2 | 81.75 | 640.5 | 640.500 | 0 |
Nous observons que la somme résidus par cette méthode est moindre. On peut donc dire que la droite passant par G1 et G2 sera meilleure que celle passant par A et B.
Cependant la calculatrice peut également nous aider à trouver l’équation de la meilleure droite.On utilisera la méthode des moindres carrés. C’est le meilleur ajustement affine qu’on puisse avoir. Nous obtenons une équation de droite y= 5.94x+154.06 et des résidus de 679,266. Nous avons ainsi la meilleure droite représentative de la croissance des levures dans ce milieu.
b) Exploitation biologique :
Le tube témoin nous sert de référence par rapport à toutes les autres expériences. Nous avons observé après avoir tracé la courbe des résultats suit une droite c’est donc une croissance linéaire.
De plus nous pouvons remarquer que cette croissance est assez rapide : en effet les levures se trouvent au nombre de 160 à t=0 et montent jusqu'à 735 à t=97. Cependant après cet intervalle de temps, de t=97 t= 114 nous remarquons un arrêt de croissance que nous pouvons interpréter par une disparition de glucose et/ou de KNOP dans la culture. Cependant, après avoir rajouté du glucose dans l’erlenmeyer nous observons un redémarrage de croissance suivant la droite de croissance déjà tracée. Nous pouvons donc supposer que le glucose avait disparu car consommé par les levures qui pourraient l’utiliser pour leur développement et pour assouvir leurs besoins nutritionnels. C’est pour cela que les expériences suivantes vont nous permettre de connaitre l’influence de glucose ainsi que du KNOP sur l’action des levures.